The High False-Positive Rate of HIV Tests
According to a 2023 National Institutes of Health (NIH)-funded article in the journal AIDS—Increased risk of false-positive HIV ELISA results after COVID-19—the false-positive rate of the HIV ELISA test is 1.3 percent (95% confidence interval).
That may not seem like much, but that is because of a common misunderstanding of what the false-positive rate represents.
The false-positive rate is not the likelihood of an inaccurate response for every positive test result; it’s the likelihood of a false-positive across all tests administered.
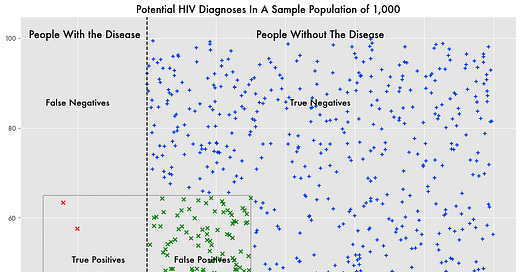
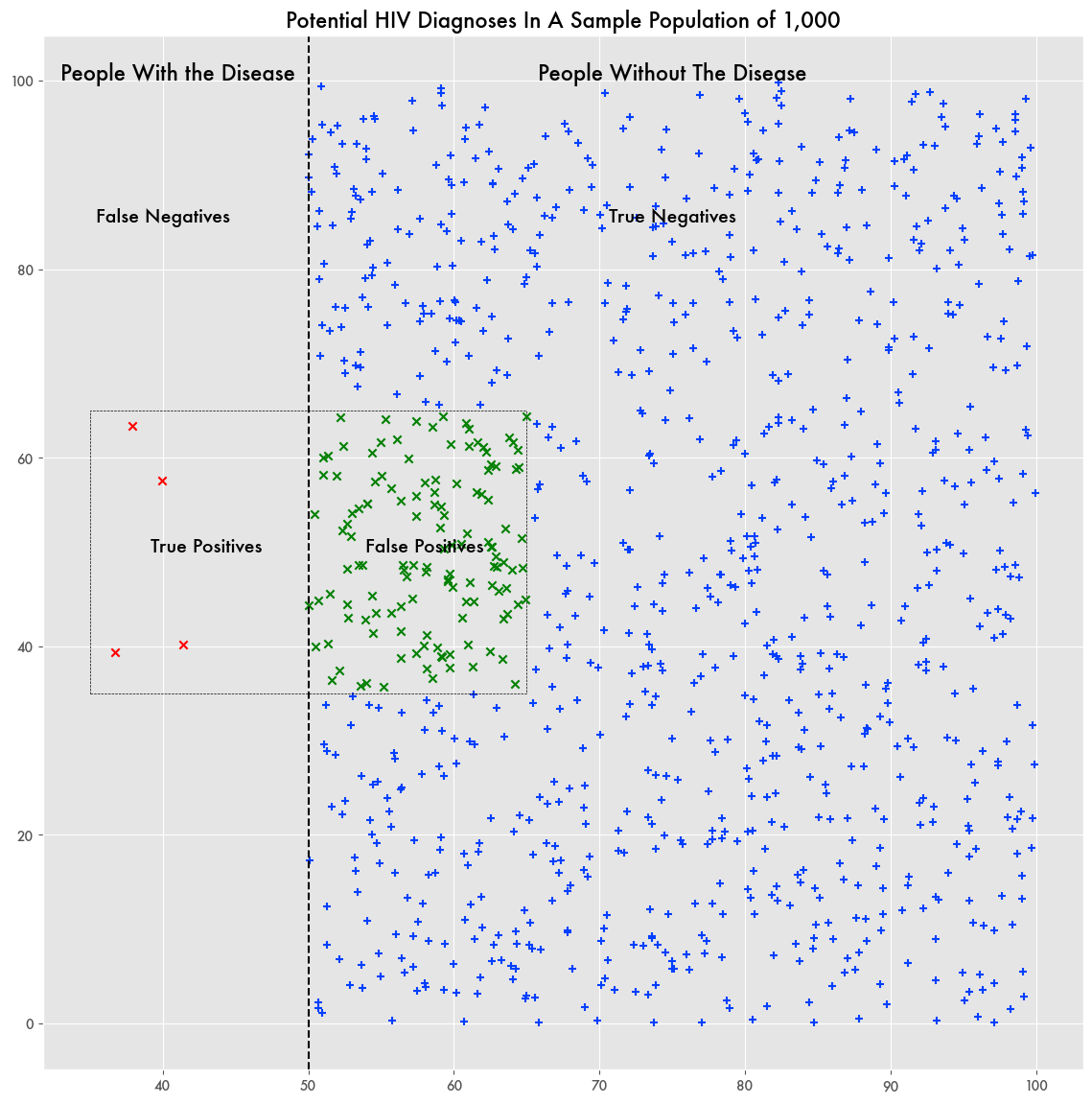
Rather than a small semantic discrepancy, it’s a significant difference when considering that the prevalence rate—the number of people who are confirmed to have HIV—is much lower than the false-positive rate—about .35 percent.
Or more simply put: a person taking the test is more likely to get a false-positive result than to actually have the disease.
The .35 percent prevalence rate is based on numbers from HIV.gov and the U.S. Census, where approximately 1.2 million people have HIV out of a population of 340.1 million (2024).
Based on the HIV test’s false-positive rate of 1.3 percent, if every American was tested, 4.42 million (340.1 million x 1.3%) would test positive despite not having the disease—significantly more than the 1.2 million that actually do.
In certain ways, the test is accurate, or more specifically, very sensitive, because it has a false negative rate of effectively zero. Almost nobody who has the disease incorrectly receives a negative result. But still, more false-positives than true positive results means that many people are falsely being diagnosed with a significant disease.
False Discovery Rate
What might be a more useful metric rather than false-positive rate would be the chance of a false-positive given a positive result, not overall, or the false discovery rate.
For that, we would need the number of true positives (accurately predicted carriers) and false-positives (inaccurately predicted carriers).
In a sample population of 10,000, there are:
35 true positives (10,000 x .35%)
130 false-positives (Note: the equation for this is slightly complicated but the end result is the same because there are no false negatives)
False Discovery Rate = False Positives/Total Number of Positive Test Results
= False Positives/(False Positives + True Positives) = 130/(130 + 35) = 78.8 percent
In general, a false discovery rate greater than 50 percent is not the marker of a reliable test.